1. Pengertian suku banyak Suku banyak atau polinom dalam variabel x yang berderajat n secara umum dapat ditulis sebagai berikut.anxn + an-1xn-1 + an-2xn-2 + …+ a2x2 + a1x + a0dengan :· an, an-1, an-2, …, a2, a1, a0 adalah bilangan-bilangan real dengan an ≠ 0.an adalah dari x2, an-1 adalah koefisien dari xn-1, an-2 adalah koefisie dari xn-2, …., demikian seterusnya. a0 disebut suku tetap (konstanta).
· n adalah bilangan cacah yang menyatakan derajat suku banyak.Derajat dari suatu suku banyak dalam variabel x ditentukan oleh pangkat yang paling tinggi bagi variabel x yang ada dalam suku banyak itu.Perhatikan bahwa suku-suku pada suku banyak diatas dawali oleh suku yang variabelnya mempunyai pangkat tertinggi, yaitu anxn. Kemudian diikuti oleh suku-suku dengan pangkat variabel x yang semakin turun, yaitu an-1xn-1, an-2xn-2, …., a2x2, a1x dan di akhiri dengan suku tetap a0. Suku banyak yang disusun atau ditulis dengan cara seperti itu dikatakan disusun mengikuti aturan pangkat turun dalam variabel x. Perlu diingat kembali bahwa variabel suatu suku banyak tidaklah harus dalam variabel x, tetapi dapat saja dalam variabel-variabel yang lain seperti variabel-variabel a, b,c …., s, t, u, …., y, z. Misalnya, suku banyak (t + 1)2 (t – 2) (t + 3) = t4 + 3t3 – 3t2 – 11t – 6 , merupakan suku banyak dalam variabel t berderajat 4. Koefisien t4 adalah 1, koefisien t3 adalah 3, koefisien t2 adalah -3, koefisien t adalah -11 dan suku tetapnya adalah -6.
Suku banyak yang hanya mempunyai satu variabel di sebut suku banyak univariabel. Selain itu ada pula suatu suku banyak dengan variabel lebih dari satu di sebut suku banyak multivariabel. Misalnya,Suku banyak x3 + x2y4 – 4x + 3y2 – 10, merupakan suku banyak dalamdua variabel ( variabel x dan y ). Suku banyak ini berderajat 3 dalam variabel x atau berderajat 4 dalam variabel y.2. Pembagian Suku BanyakBentuk UmumF(x) = P(x).H(x) + S(x)F(x) = suku banyakP(x) = pembagiH(x) = hasil bagiS(x) = sisaa. Teorema Sisa:Jika suatu suku banyak F(x) dibagi oleh (x – k) maka sisanya adalah F(k)Jika pembagi berderajat n maka sisanya berderajat n – 1Jika suku banyak berderajat m dan pembagi berderajat n, maka hasil baginya berderajat m – nCara Pembagian Suku BanyakContoh:F(x) = 2x3 – 3x2 + x + 5 dibagi dengan P(x) = 2x2 – x – 1a. Pembagian biasa
Jadi hasil baginya: H(X) = x – 1, sisanya S(x) = x + 4b. Cara Horner/Skemabisa digunakan untuk pembagi berderajat 1 atau pembagi yang dapat difaktorkan menjadi pembagi-pembagi berderajat 1Cara:- Tulis koefisiennya saja → harus runtut dari koefisien xn, xn – 1, … hingga konstanta (jika ada variabel yang tidak ada, maka koefisiennya ditulis 0)
- Jika koefisien derajat tertinggi P(x) ≠ 1, maka hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
- Jika pembagi dapat difaktorkan, maka:
H(x) = 1.x – 1 = x – 1S(x) = P1.S2 + S1 = (2x + 1).1/2 + 7/2 = x + ½ + 7/2 = x + 4c. Cara koefisien tak tentuF(x) = P(x).H(x) + S(x)Untuk soal di atas, karena F(x) berderajat 3 dan P(x) berderajat 2, makaH(x) berderajat 3 – 2 = 1S(x) berderajat 2 – 1 = 1Jadi, misalkan H(x) = ax + b dan S(x) = cx + dMaka:2x3 – 3x2 + x + 5 = (2x2 – x – 1).(ax + b) + (cx + d)Ruas kanan:= 2ax3 + 2bx2 – ax2 – bx – ax – b + cx + d= 2ax3 + (2b – a)x2 + (–b – a + c)x + (–b + d)Samakan koefisien ruas kiri dan ruas kanan:x3 → 2 = 2a → a = 2/2 = 1x2 → –3 = 2b – a → 2b = –3 + a = –3 + 1 = –2 → b = –2/2 = –1x → 1 = –b – a + c → c = 1 + b + a = 1 – 1 + 1 → c = 1Konstanta → 5 = –b + d → d = 5 + b = 5 – 1 → d = 4Jadi:H(x) = ax + b = 1.x – 1 = x – 1S(x) = cx + d = 1.x + 4 = x + 43. Teorema FaktorSuatu suku banyak F(x) mempunyai faktor (x – k) jika F(k) = 0 (sisanya jika dibagi dengan (x – k) adalah 0)Catatan: jika (x – k) adalah faktor dari F(x) maka k dikatakan sebagai akar dari F(x)Tips:
- Untuk mencari akar suatu suku banyak dengan cara Horner, dapat dilakukan dengan mencoba-coba dengan angka dari faktor-faktor konstantanya ang akan memberikan sisa = 0
- Jika jumlah koefisien suku banyak = 0, maka pasti salah satu akarnya adalah x = 1
- Jika jumlah koefisien suku di posisi genap = jumlah koefisien suku di posisi ganjil, maka pasti salah satu akarnya adalah x = –1
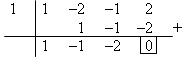Jadi x3 – 2x2 – x + 2 = (x – 1)(x2 – x – 2)= (x – 1)(x – 2)(x + 1)x = 1 x = 2 x = –1Jadi himpunan penyelesaiannya: {–1, 1, 2}4. Sifat Akar-Akar Suku BanyakPada persamaan berderajat 3:ax3 + bx2 + cx + d = 0 akan mempunyai akar-akar x1, x2, x3dengan sifat-sifat:- Jumlah 1 akar: x1 + x2 + x3 = – b/a
- Jumlah 2 akar: x1.x2 + x1.x3 + x2.x3 = c/a
- Hasil kali 3 akar: x1.x2.x3 = – d/a
- Jumlah 1 akar: x1 + x2 + x3 + x4 = – b/a
- Jumlah 2 akar: x1.x2 + x1.x3 + x1.x4 + x2.x3 + x2.x4 + x3.x4 = c/a
- Jumlah 3 akar: x1.x2.x3 + x1.x2.x4 + x2.x3.x4 = – d/a
- Hasil kali 4 akar: x1.x2.x3.x4 = e/a
Tidak ada komentar:
Posting Komentar